2. Булева алгебра, множества, особенности сравнения объектов.

На прошлом уроке мы уже знакомились с булевым типом данных.

Переменная типа bool может содержать только два значения: True или False, при чем это не строки, не числа, а именно понятия ложь и истина.

Для работы с булевыми переменными существует булева алгебра.

Булева алгебра (логические операторы)

Существуют следующие логические операторы:

and - И
or - ИЛИ
xor - Исключающее ИЛИ (подключается отдельно)
not - НЕ

not означает НЕ, и, будучи поставленным перед типом bool, меняет его значение на обратное, т.е. not True становится False,not False становится True

Далее приведена таблица, демонстрирующая работу операторов:

	0 to 1	1 to 0	1 to 1
and	0	0	1
or	1	1	1
xor	1	1	0

Оператор условия если (if)

Во многих, если не во всех языках программирования существуют условия вида если - иначе, если - иначе. Код выглядит примерно следующим образом:

если (X mod 2 == 0):
    число нечетное
иначе:
    число четное

Операция mod - операция взятия остатка от деления.

Есть различные варианты использования оператора если: просто если, с использованием иначе и с любым количеством иначе, если между если и иначе, если.

Тернарные операторы

Во многих языках программирования (С++, Java, PHP...) существуют тернарный оператор, т.е. специальный оператор условия, который возвращает один из двух результатов, в зависимости от того, выполняется его условие или нет. Выглядит он так:

сообщить (Время суток = 'утро') ? "Привет!" : "Пока!";

Тернарные операторы часто применяются, когда варианта всего два, так как такая запись короче аналогичного действия с если. Однако, к сожалению, можно встретить связку нескольких если и тернарных операторов, которую совершенно невозможно прочесть. Другими словами, это не необходимая вещь в языке и она может стать причиной нечитаемого текста.

Множества

Множество или сет (set) по сути - "контейнер", содержащий не повторяющиеся, уникальные элементы в случайном порядке. В этом определении упомянуты две основные особенности сетов - уникальность и отсутствие сортировки.

Уникальность - сет содержит только уникальные элементы, если добавлять в него дубликаты - они не добавляются, если перевести какую-то переменную с неуникальными данными в сет - дублирующие элементы будут удалены.

Отсутствие сортировки - элементы в сете находятся в неком хаотичном порядке.

Множества поддерживают перебор всех элементов (итерацию), добавление и удаление элементов, но в силу отсутствия сортировки не поддерживают индексацию и срезы.

Создание множеств:

м1 = множество([1, 2, 3, 4, 5, 6])
м2 = множество([5, 6, 7, 8, 9])

a = [1, 2, 3, 4, 5, 6, 5, 4, 3, 2]
вывести a
[1, 2, 3, 4, 5, 6, 5, 4, 3, 2]
м3 = множество(a)
вывести м3
([1, 2, 3, 4, 5, 6])

Множества поддерживают операции вычитания, объединения, пересечения:

 м1 = множество([1, 2, 3, 4, 5, 6])
 м2 = множество([5, 6, 7, 8, 9])
м1 - м2 # Разность множеств
([1, 2, 3, 4])

м1 | м2 # Объединение множеств
([1, 2, 3, 4, 5, 6, 7, 8, 9])

м1 & м2 # Пересечение множеств
([5, 6])

Можно добавить элемент в множество и удалить из множества элемент. В качестве параметра выступает сам элемент, поскольку индексов в множестве нет.

м1.добавить(7)
вывести м1
([1, 2, 3, 4, 5, 6, 7])
м1.удалить(1)
вывести м1
([2, 3, 4, 5, 6, 7, 8])

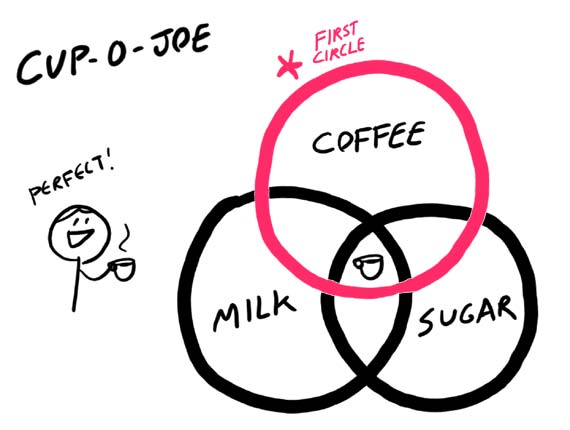
Круги Эйлера

Множества принято визуализировать при помощи кругов Эйлера.

Практические задания на круги Эйлера

1. Разместить в кругах:

Числа целые
Числа положительные
Числа отрицательные
Числа простые

2. Нарисовать круги для заварного кофе:

эспрессо
американо
каппучино
латте
доппио

3. Решить задачу: Все женщины - дочки, но не все женщины матери. Некоторые матери - бабушки. Нарисуйте внучек!

5. Разместить в кругах: Зайцы четвероногие, млекопитающие, хордовые, живородящие. Лебеди птицы, яцекладущие, хордовые. Утконосы четвероногие, яйцекладущие, млекопитающие.

5. Разместить в кругах: Всего Студентов 2000 Программистов 1500 Дизайнеров 300 Менеджеров 200 Фронтендщиков 1000 Бекендщиков 500 PHP программистов 200 JS программистов 1100 Java программистов 100

Полезные ссылки

Доп. статьи:

Математическая логика Решания задач при помощи кругов Эйлера Тест на логическое мышление Онлайн создание диаграмм

Домашка

Домашнее задание

Basics_02.md 7.9 KB Cronologia Originale